OWASP LATAM@home : HTTPS
11/05/2020Al parecer mi generador de claves RSA tiene vulnerabilidades
Análisis inicial
Como parte del reto recibimos un único archivo, correspondiente a una captura de tráfico TLS, presuntamente HTTPS. Al tratarse de un reto de crypto y en base a la descripción del problema, podemos suponer que se trata de alguna debilidad en la generación de las llaves usadas para cifrar el tráfico.
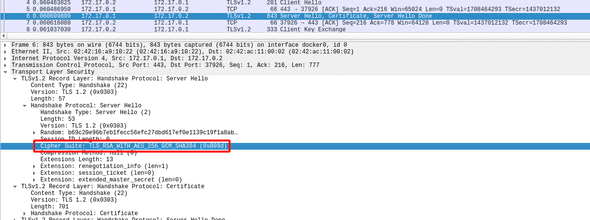
Un análisis rápido del archivo nos permite identificar dos streams de datos en conexiones separadas, ambas utilizando como juego de algoritmos TLS_RSA_WITH_AES_256_GCM_SHA384, como puede verse en el paquete Server Hello de cada una:
Extracción de llaves públicas
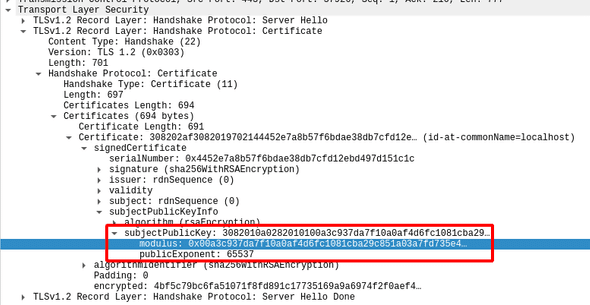
TLS está haciendo uso de RSA, que de acuerdo a la descripción del problema debiera ser nuestro objetivo. Para extraer la llave pública de cada conexión, podemos expandir la sección del paquete Sever Hello respectiva, y encontrar el módulo (n) y exponente público (e).
Haciendo esto para ambos streams, vemos lo siguiente:
| e | n | |
|---|---|---|
| Stream 1 | 65537 | 0x00a3c937da7f10a0af4d6fc1081cba29c851a03a7fd735e4a07bb… |
| Stream 2 | 65537 | 0x00965d6a37f4a6b1e0f63603fca2fbb8cf9005414db33e1c65130… |
Los módulos RSA utilizados son distintos, pero lo suficientemente largos como para evitar ser facilmente factorizables. Si los módulos han sido generados utilizando primos en común, es posible factorizar ambos de manera simultánea buscando su máximo común divisor (GCD).
Factorizando ambos módulos vía GCD
Recordemos que el módulo n de una llave RSA se genera tomando dos números primos grandes p y q y obteniendo su producto. En nuestro caso tenemos n1 y n2, los módulos correspondientes a ambos streams, donde:
n1 = p1 * q1
n2 = p2 * q2Si ambos módulos tuvieran un número primo en común, por ejemplo p1 = p2, en lugar de tener dos problemas de factorización de números grandes completamente independientes y extremadamente difíciles de resolver, terminamos en un sólo problema de encontrar el factor común entre dos números, que es computacionalmente sencillo. Esto nos permite derivar el factor p común a ambos módulos, y por tanto derivar las llaves privadas de ambos streams al mismo tiempo. La implementación en python, usando gmpy2 es tan simple como:
from Crypto.PublicKey import RSA
import gmpy2
n1= 0x00a3c937da7f10a0af4d6fc1081cba29c851a03a7fd735e4a07bb87ae764dd34138f229038caedf1c28bae19772f389f5cd2e7a23ddb2773a5d1203377748c997d7ffd0de779fd723b60d608d7bbbcf4434a35541e601f0159ada7afe9e066120881682468397e2c361ed23e1bb948ed63fd8be4cb6037569d455b4ea9e79e283834baa3fa4477aa56a0214860babb7bee47dcacb1efdfdb79c79a4bea5263f5b8d9e6f5184ce4d0dfa0af9822e090656989b6ef9bac132a0e1367e175c0d565f46266c818ced5b5256fcf5b0a8d52442e75932bc9a0f794dca1397dccf6cb350d76a6c08dfdb4e4936da254bcc350ab8a0fe3182030dffc2b202b8cd71f9ace95
n2 = 0x00965d6a37f4a6b1e0f63603fca2fbb8cf9005414db33e1c65130b56a28e3486bd82c82c173ca1f811523b929c3b65822d870ad36c7214fd42990a83b3e13c1f0851ed57fc2ff4dc4a9187526471c5acd230e03da4ba0b7fddef43e7046b43500223d161013b8409407286fc597ef445ceb9a23dde2fa6df2d1134c53072d2161a77ef0cb25374ad00c7f0ee54a23c2f39e9fd9097e1333d3449095948125ffec25435b217ba124f71ae2fd0b2b116682ab7186e80077e76512d7700adc1953abb26646e006722e1cbf0ba5b090e558ff51c332565061a67e788c07d80adc0d613683f112fa389029ee3c012a9df92cf684c0eab317ef76acd8a9bfe896f904b2d
e=65537
p = gmpy2.gcd(n1,n2)
print(p) # si p == 1, no existe un primo común
q1 = n1 // p
q2 = n2 // p
phi1 = (p-1)*(q1-1)
phi2 = (p-1)*(q2-1)
d1 = int(gmpy2.invert(e,phi1))
d2 = int(gmpy2.invert(e,phi2))
privkey1 = RSA.construct((n1,e,d1))
privkey2 = RSA.construct((n2,e,d2))
with open("k1.key", 'wb') as content_file:
content_file.write(privkey1.exportKey('PEM'))
with open("k2.key", 'wb') as content_file:
content_file.write(privkey2.exportKey('PEM'))Esto debiera generar dos archivos con las llaves privadas en formato PEM, listo para utilizar en wireshark o cualquier otra herramienta.
Descifrando el tráfico en wireshark
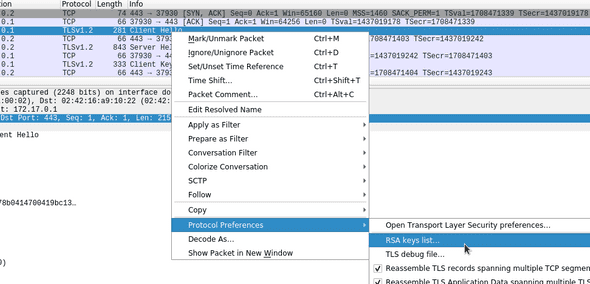
Tomando el primer stream, damos clic derecho sobre cualquier paquete de tipo TLS y nos dirigimos al siguiente menú:
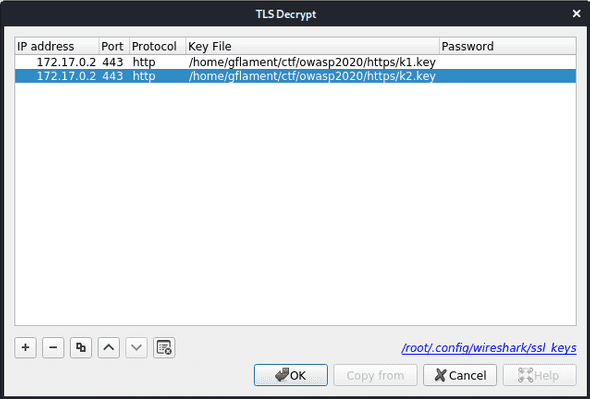
Procedemos a añadir ambas llaves, indicando la dirección del servidor que genera el tráfico a descifrar, así como el puerto de la conexión TLS y el protocolo en texto plano utilizado:
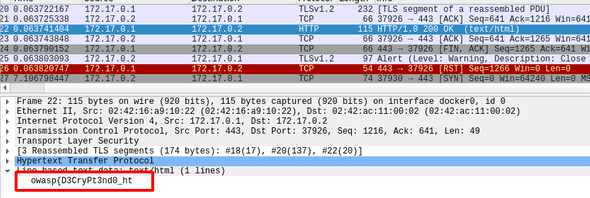
Y podemos leer el flag que se encuentra dividido en dos partes, una en cada stream: